Más contenido relacionado
การแก้ปัญหากำหนดการเชิงเส้นโดยใช้กราฟ
- 1. การแก้ปัญหากาหนดการเชิงเส้นโดยวิธีการใช้กราฟ
ในการแก้ปัญหากาหนดการเชิงเส้นนั้นต้องเริ่มต้นด้วยการสร้างแบบจาลองทางคณิตศาสตร์ ซึ่ง
ประกอบด้วย 2 ส่วน คือ
ส่วนที่ 1 ส่วนที่เป็นเป้าหมาย จะอยู่ในรูปของ สมการจุดประสงค์ (ในเอกสารเล่มนี้ใช้ P)
ส่วนที่ 2 ส่วนที่เป็นข้อจากัด จะอยู่ในรูปของ อสมการข้อจากัด
ซึ่งเป็นการแปลงสถานการณ์ปัญหาให้เป็นปัญหาทางคณิตศาสตร์ จากนั้นจึงหาคาตอบของปัญหา
ด้วยวิธีการต่าง ๆ ในการศึกษาครั้งนี้ใช้การกราฟช่วยในการหาคาตอบ
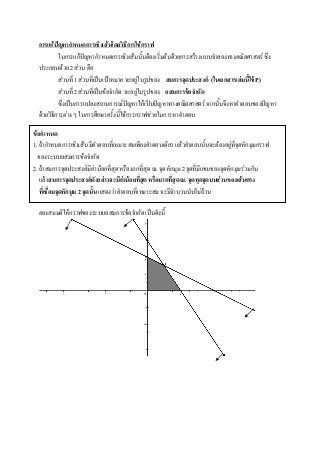
ลองสมมติให้กราฟของระบบอสมการข้อจากัด เป็นดังนี้
ข้อกาหนด
1. ถ้ากาหนดการเชิงเส้น มีคาตอบที่เหมาะสมเพียงคาตอบเดียว แล้วคาตอบนั้นจะต้องอยู่ที่จุดหักมุมกราฟ
ของระบบอสมการข้อจากัด
2. ถ้าสมการจุดประสงค์มีค่าน้อยที่สุด หรือมากที่สุด ณ. จุดหักมุม 2 จุดที่มีแขนของจุดหักมุมร่วมกัน
แล้วสมการจุดประสงค์ดังกล่าวจะมีค่าน้อยที่สุด หรือมากที่สุด ณ. จุดทุกจุดบนส่วนของเส้นตรง
ที่เชื่อมจุดหักมุม 2 จุดนั้น แสดงว่าคาตอบที่เหมาะสม จะมีจานวนนับไม่ถ้วน
- 2. นาความจริงจากข้อกาหนดมาวิเคราะห์ กราฟของระบบสมการข้อจากัดดังนี้
1. จุดทุกจุดในบริเวณส่วนที่แรเงาจะสอดคล้องกับระบบอสมการข้อจากัด ถูกเรียกว่า
“เซตของคาตอบที่เป็นไปได้”
2. จากเซตของคาตอบที่เป็นไปได้ เราจะนาไปหาจุดใดที่สดคล้องกับสมการจุดประสงค์ที่ให้ค่าน้อยที่สุด
หรือค่ามากที่สุดจากกราฟของระบบอสมการข้อจากัด
3. จุดทุกจุดในบริเวณส่วนที่แรเงา มีโอกาสเป็นไปได้ที่จะทาให้สมการจุดประสงค์มีค่าน้อยที่สุด
หรือมากที่สุด แต่จุดหักมุมมีโอกาสเป็นไปได้มากกว่า
4. จุดในบริเวณส่วนที่แรเงาที่ทาให้สมการจุดประสงค์มีค่าน้อยที่สุดหรือมากทีสุดถูกเรียกว่า
คาตอบที่เหมาะสม
5. ถ้ากาหนดการเชิงเส้นมีคาตอบเดียว แล้วจุด A,B,C และ O จุดใดจุดหนึ่ง จะทาให้สมการจุดประสงค์
มีค่าน้อยที่สุด หรือมากที่สุด
6. ถ้าจุด A และ B ทาให้สมการจุดประสงมีค่าน้อยที่สุด แล้ว จุดทุกจุดที่อยู่บนส่วนของเส้นตรง AB จะทา
ให้สมการจุดประสงค์ มีค่าน้อยที่สุดหรือมากที่สุดด้วย แสดงว่าคาตอบที่เหมาะสมจะมีจานวนนับไม่ถ้วน
อ้างอิง
https://krusand.files.wordpress.com/2014/06/e0b980e0b899e0b8b7e0b989e0b8ade0b8abe0b8b2e0b
881e0b8b3e0b8abe0b899e0b894e0b881e0b8b2e0b8a3e0b980e0b88ae0b8b4e0b887e0b980e0b8aa
e0b989.doc